Table of Contents
Welcome to the sixth article of the Sonic Battle (GBA) Renderer series.

Camera
Background info
A general camera system is described in Joey de Vries’ learnopengl.com series:
Specific
For reference, here’s the coordinate system used in this series.
Our camera has very little “primary” state. The state that the user can set is:
- Position in 3D space
- Heading (rotation around the Z axis)
- Pitch (rotation around the X axis)
It also contains “secondary” state which is derived once per frame from the primary state:
- Facing direction in 3D
- Facing direction in 2D (on the XY plane)
- Transformation matrix and its inverse (the inverse is the conventional view matrix)
Transformation matrix
- Create translation matrix using position
- Apply heading rotation
- Apply pitch rotation
In conventional matrix notation this would be: translationMatrix * headingMatrix * pitchMatrix.
The GLM math library takes care of the specifics. A few details:
- Base axis rotation (like rotation around the Z or X axis) is a special case which can be computed cheaply. GLM’s euler angle functions are used for that.
- The inverse can be computed from a mat3, then casted back to mat4 and multiplied with the opposite translation matrix (mat3 inverse is a ton faster than the mat4 inverse)
Facing direction in 2D
vec(cos(heading), sin(heading))
(Using the trigonometric circle.)
Facing direction in 3D
- The default direction is
vec(0, 1, 0, 0) - The 3D direction is
transformMatrix * defaultDirection
Which simplifies to just taking the second column of the transformation matrix.
Note - canvas space
I’ll ommit the subject of canvas/screen space (see this note for details). For the sake of simplicity the series will treat view/camera space as the final space for rendering.
Tilemap
To render a tilemap we need to compute its affine matrix and its view-space position.
We’re dealing with two tilemaps (bottom and top). They can both use the same affine matrix because only their positions differ.
View-space position
First, to get the view-space (or camera-space) position:
camera.transformMatrixInverse * worldSpacePosition
Affine matrix
Our affine matrix is a 2D (2x2) matrix. To compute it we:
- Create a scale matrix from
vec(1, cos(camera.pitch)) - Apply rotation to it using the opposite of the camera heading
In conventional matrix notation this would be: pitchScaleMatrix * oppositeHeadingRotationMatrix.
Scale logic
The orthographic projection used by the renderer can be represented by vector projection. In the case of unit vectors, by a dot product more specifically.
The tilemap’s normal vector needs to be projected on the opposite of the camera’s direction.
The algebraic dot product formula for 3D vectors is v1.x * v2.x + v1.y * v2.y + v1.z * v2.z.
We deal only with the YZ plane here, so let’s ignore x: v1.y * v2.y + v1.z * v2.z.
The tilemap normal is vec(0, 0, 1). Let’s plug it into our 2D formula (v1 would be the tilemap normal, and v2 the opposite of the camera direction): 0 * v2.y + 1 * v2.z which simplifies to v2.z. This is cos(camera.pitch - pi) (the minus pi accounts for the opposite direction).
We’re not quite done though. Because we want to look towards +Z by default instead of -Z, we need to use the opposite direction again. So we get cos(camera.pitch - pi - pi) which simplifies to cos(camera.pitch).
Scale logic sketch
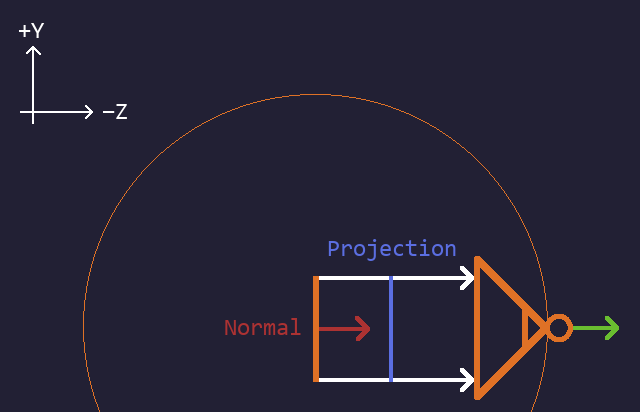
Camera pitch = 0 degrees

Camera pitch = 45 degrees
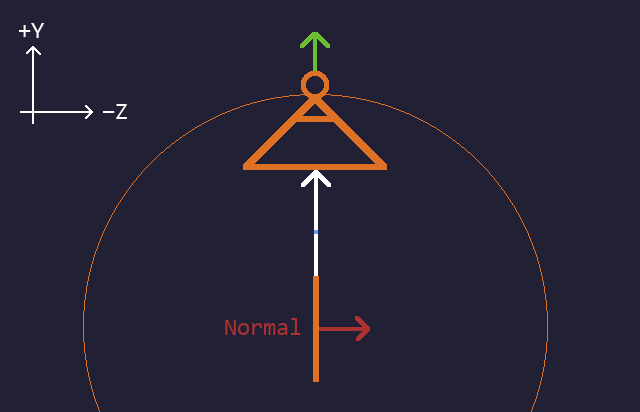
Camera pitch = 90 degrees
Visualization
Scale
Rotation
Scale and rotation
The next article deals with walls (“how to transform the 2D surfaces to make them to look 3D”).